Nodes by hexnet

Woodblock frontispiece from the Diamond Sutra, printed during the Tang Dynasty, and considered—by Wikipedia and the British Library—to be the oldest dated printed book in the world. Dated to the year AD 604; (868.).

We clearly see in this woodcut the use of a pseudo-hexagonal background matrix of some sort. This is perhaps an allusion not only to the hexagonal structure of diamond itself, but also to the adamantine nature of hexagonal geometry.

Breaking news from the world of HEXAGONS:

While reviewing the hexagonal news this morn, I ran across an article describing some sort of Hexagon Project out of Scranton, Pennsylvania. Looking into it further, I expected to find that—like many hexagon-identified things these days—the "hexagon" was a purely metaphorical branding feature. To my surprise though, it not only involves literal hexagons, but the hexagonal geometry seems to have been deliberately and consciously chosen for very hexagonally-aware reasons. The project's page explains, under the heading "Why a hexagon?":

"The hexagon is a composition of complex relationships, interdependent lines, like bonds of human connection, strengthened in multiples into an infinite network of connections. It maintains its own presence as a shape, symbol of light and life, yet, structurally, destined to be part of a whole—a splendid architectural element, infinitely expandable."

[Edit 2013-10: The existence of this post has bothered me since I first published it three years ago. Basically, this was intended as the first installment of what was to have been a sprawling series of posts attempting to reconcile what I will loosely term "Eastern monism" with the semantically precise, mathematical ontology I have been trying to develop in light of hexagonal principles—and in a real, meaningful way, not just in some fake-ass pop quantum mysticism sense. I won't recapitulate my whole line of thought here, but suffice to say I had and continue to have more substantive and I think relevant ideas on these matters than those expounded in this limited post, which by itself I think ends up conveying either that I misunderstand or misinterpret people like Watts, or that I am not particularly interested in the finer implications of what they tried to communicate. And I would like to think neither is true. Watts was a huge intellectual influence on me in my youth, and it was writings such as his that actually turned me from my earlier phase of hexagonal thinking as a teenager—only to return to it with more clarity of thought over a decade later. And having later become of aware of his passing references to hexagons, I was very eager to draw out these ideas and sort of riff on them with the greater perspective gained from the ensuing years. But I left the task unfinished, and, again, I think this post, by itself, is sort of weird. I gave serious thought to deleting it or leaving it unpublished in this latest iteration of the site, but ultimately decided to leave it here, with this disclaimer. I intend to revisit these issues at some point, hopefully in greater detail, at which point I will perhaps modify or edit this post further.]

"Where is it writ large that talking monkeys should be able to model the cosmos?" – Terence McKenna

I remember reading a short but eloquent endorsement of hexagons by Alan Watts once, probably seven or eight years ago. Since I wasn't particularly interested in hexagons at the time, I quickly forgot about it, and where exactly I had read it. However, times have changed and my hexagonal thinking has evolved, and with the advent of Google Books and all, I recently decided to look into the matter further. After an exhaustive search, I found two mentions of hexagons in Watts' books, which I shall now share with you, and duly expound upon.

I am not entirely sure either of these is in fact the passage I remember reading, but if it were either of them it would be this first one, which can be found in the essay What on Earth Are We Doing?, from the collection Cloud-Hidden, Whereabouts Unknown:

“When the going gets weird, the weird turn pro.” – Hunter S. Thompson

The last components necessary to make this site passably acceptable to me were completed last evening. Thus, as promised, on time and under budget, I hereby declare this site to exist. Several important facts to keep in mind:

First and foremost, the site is of course not really done. Also it still sort of sucks. But it is functional enough that it stands on its own, does not have any overtly malfunctioning content, and generally seems to work pretty well, so rather than delaying any longer I am just going to put it out there. But I expect to be adding many useful and pertinent features and content items in the coming weeks and months. So check back often or something.

An astute reader recently brought to my attention the nascent movement afoot to replace π in common usage with the number now unfortunately known as 2π—viz., 6;349419 (dec. 6.283186):

• Pi Is Wrong! - By Bob Palais
• The Tau Manifesto - By Michael Hartl

(For a reasonably convincing argument on why the letter τ (tau) in particular should be adopted for this value, please read Mr. Hartl's manifesto.)

The fundamental point here is that, in trigonometry and all other manner of angle-measuring endeavors, what we care about is the radius of a circle, not its diameter. The one follows from the other to be sure, but at the end of the day the diameter is more usefully considered twice the radius than the radius is half the diameter. A circle is a circumference around a center—it is the measure of this distance between center and circumference that is elemental to the idea of a circle, not the rather incidental fact that its full width is twice that same distance.

This is a unit circle diagram using both dozenal notation (as with elsewhere on this site, using "A" and "B" for ten and eleven) and the newly proposed circle constant τ (tau), which is equal to 2π. The advantages of τ over π are numerous and obvious—instead of a full circle of arc being two of anything, it is just one τ. Put another way, τ is simply the number of radians in a circle.

I seem to have taken an unintentional hiatus from putting my ass into this project, due largely to the fact that it has of late been too hot to move, think, or do anything at all really. Come hell or high water though, I will "launch" this site by the first of Sextilis, being actually the fifteenth (13th;) anniversary of the launch of my first Hexnet site, back in 1995. That is probably an unnecessarily dramatic theme to tie in with this whole procedure, but it seems silly to allow such an auspicious date to pass unobserved. Also, I really need to get on with this. I mean, I have numerous medium-term goals to tweak the layout—I want to clean up and expand the links section, among other things—but most of that can wait. I am really just trying to wrap up a bit of library content, actually. Which at this point seems fairly silly, since I long ago gave up on my original idea of having some sort of centralized "Hexagonal Manifesto" or what have you, in favor of a more modular if somewhat disjointed collection of one-off content items and such. Anyway, since 1 August falls lamentably on a Sunday this year, which is a terrible day to do anything PR-wise (as is the entire month of August, really), I expect to do some sort of formal what have you by next week some time. Or you know whenever.

That is all. Thank you for your attention

Robert Indiana's "Eternal Hexagon."

Here we see the well-known icosahedral version of R. Buckminster Fuller's dymaxion map projection of the earth's surface. A similar projection can be created by mapping the globe onto any other convex polyhedron, and unfolding it into a flat net of polygons. This particular icosahedral net has become widely used due to its relatively contiguous and undivided treatment of the earth's land mass, which for general cartographic purposes is often seen as useful. However, other nets—icosahedral and otherwise—exist that accentuate and prioritize other aspects of the earth's surface, such as the oceans.

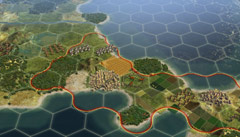Anyone following the hexagonal news of late has no doubt noticed a flurry of stories related to the upcoming release of Civilization V, and in particular its new hexagonal tile system. In this blog's opinion, the adoption of hexagonal tiles by the Civ franchise is a long overdue development, and frankly one that should've been incorporated into at least the last two Civ releases. Indeed, many DOS-based strategy games have used hexagonal tiles going back to the late '80s, and one has to wonder why Civilization ever used square tiles. (I remember playing the original Civilization in the early '90s, well before the advent of my own hexagonal illumination, and thinking that, in fact, it would be better with a hexagonal grid. I can only imagine part of the media excitement here—aside from just the general awesomeness of hexagons—is due to the fact that many, many other people have had the exact same thought over the past twenty years.)

Recent advances in microscopy have allowed the direct imaging of molecular bonds for the first time. Here we see several images highlighting the hexagonal structure of several hydrocarbons.

Here we see the original illustration of the Five Fingered Hand of Eris from the Principia Discordia.

Quoth the Principia:

"The official symbol of POEE is here illustrated. It may be this, or any similar device to represent TWO OPPOSING ARROWS CONVERGING INTO A COMMON POINT. It may be vertical, horizontal, or else such, and it may be elaborated or simplified as desired.

NOTE: I have transcribed and edited this from various ancient translations of Euclid, augmented and tempered where necessary by at least the structure of more modern versions. I am pretty sure there are no errors in it. This is of course only one of many interesting Euclidean propositions involving hexagons, and for anyone reading this who does not in fact own a copy of Euclid I highly recommend purchasing one right now. Thank you.

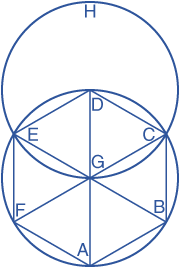Let ABCDEF be the given circle. It is required to inscribe an equilateral and equiangular hexagon in the circle ABCDEF.

I have been reading about the PAH world hypothesis, and have come to see it as an intriguing indicator of the potentially hexagonal origins of life on earth.

Essentially, it is conjectured that, since polycyclic aromatic hydrocarbons are among the most common spaceborne molecules in the known universe, they would have likely been a constituent in the primordial seas of Earth, where they could have provided some sort of scaffolding or template on which early biological polymers such as RNA could assemble, thus solving a frequently-raised objection to the RNA world hypothesis that RNA is too fragile and transient to survive long outside of an extant cell or similar protective environment. By providing a structural backbone on which reasonably complex RNA strands and such could self-assemble, the PAH world would have given early pre-cellular life a fighting chance of finding its way into protective lipid bubbles, weird mineral formations, or what have you, where given enough replicative iterations it presumably developed into proper cellular life as we know it.

Here we see illustrated the the principle that, for any given natural number n, the sum of the first n centered hexagonal numbers is equal to the cube of n. In this particular example, 1+7+19+37=4^2=64. In the color scheme above, the first hex number corresponds to the blue cube on the vertex of the cube figure, while the seven cubes of second hex number represent the purple shell of cubes behind this, and so on—one can easily visualize how the number of units in any particular hex number correspond to the equivalent shell of cubes.

The Tetractys is a triangular figure of ten points arranged in four rows, equivalent to the fourth triangular number. It was considered sacred by the ancient Pythagoreans of yore.

Here we see the well-known "Flower of Life" pattern, consisting of nineteen interlocking hexagons in a cubic/hexagonal arrangement. While the particular term "Flower of Life" is, as far as I have ever been able to determine, of fairly recent and dubious origin, there is certainly no doubt that the pattern itself is of great antiquity, and can be found throughout the world among many different cultures.

Metatron is an angel described in Jewish and other Abrahamic religious texts, variously identified as the Scribe of God, the Lesser Tetragrammaton, et cetera. He/it is closely identified with the prophet Enoch, and by many accounts they are one and the same entity.

The cube itself consists of thirteen (doz. 11) circles, six of which emanate out from seven hexagonally packed circles in the center, with line segments connecting the center of each circle with the center of every other circle. This has the effect of producing a highly hexagonal pattern onto which one can map orthographic projections of all five Platonic solids. Note that this figure can also be expressed in the form of an actual cube, which sixteen (doz. 14) spheres instead of thirteen circles.

Here we see the classic Adidas Telstar ball from the 1970 World Cup. Said World Cup was the first to be televised live, and the ball was given contrasting colors to improve its visibility on television (hence the name). Although Adidas has unfortunately moved away from this classic icosahedral design in recent World Cup balls (a decision I believe they will come to regret), the Telstar remains the archetypal soccer ball design in popular culture, due presumably to the enduring aesthetic appeal of its hexagonal geometry. Modern balls that do not feature an actual contrasting color tiling often still use truncated icosahedral panels, presumably due to their structural superiority over other methods of ball enclosure.

Here we see the hexagonal architecture of the International Space Station's Cupola module. Hexagonal space-windows are often seen in science fiction treatments of space travel, but this is the first time we have seen a proper full-sized hexagonal window in an actual spaceborne craft. The hexagon is of course the natural geometry for dealing with the hostile environemnt of outer space, as we have seen for many decades now in the hexagonal structure of satellites and deep space probes. No doubt we will see more and more such hexagonal architecture as we move out into the Solar System—eventually.

A centered hexagonal number, or hex number, is a centered figurate number that represents a hexagon, with an original dot in the center representing the first order hex number, and additional dots added in concentric rings representing successive hex numbers, forming a hexagonal lattice, or packing of circles, depending on your spatial metaphor of choice. In decimal, the first few centered hexagonal numbers are: 1, 7, 19, 37, 61, 91, 127, 169, 217, 271, 331, 397, and so on.

It looks like the hexagonal zeitgeist is finally floating to the surface of our collective media environment. Two stories in particular off of our hexagonal news feed caught my eye this morn:

Geometry lessons
". . . Just as the 1950s will always be remembered as the decade of atomic-inspired motifs, so may the early decades of the 21st century be remembered, by those of pop cultural bent, as belonging to the hexagon."

The Hexagon Harley 1.4301
"Six is the magic number on this handcrafted custom Harley Davidson by Horst Dzhangmen. Everything but the engine, a HD Shovelhead 1340 cm3 and the frame, has been cut and built into perfectly shaped hexagons and this exceptional work took its creator three years of hard work to achieve this perfection."

Here we photo of a hexayurt built for Burning Man, assembled in a backyard somewhere north of Davis Square, and a diagram of standard hexayurt dimensions provided by the Hexayurt Project.

Here we see a pleasing assortment of wasps constructing new colonies with naught but hexagons and saliva.

In this image we see the classic hexagonal honeycomb structure of the enlightened honeybee. The hexagonal structure is common to the nesting architecture many related insects, including wasps, et cetera. Note that the strength of the comb is improved not only by the superior hexagonal geometry, but also by the skillful employment of rhombic facets at the closed end of the cells.

This site is not yet completed, and at least one core content piece is still in progress, but after some months of halfassery, I am prepared at this time to move into Phase I of my three-phase site launch program. This site is live as of May 30, 2010 (May 26, 11B6), and hopefully shall remain so. FTVW.

Again, I cannot overemphasize how not-ready-for-formal-launch this site is. Structurally, several site elements still need some work, and as I said some content is still being developed, including my short mathematical summary of hexagons, which, though somewhat trivial, arguably constitutes a somewhat significant piece of content on a site nominally about hexagons.

Hopefully we will be ready to proceed to Phase II within the next week. Thank you.

Several images of hexagonal geodesic dome structures at the Eden Project in Cornwall, Britain.

"Wilson Alwyn "Snowflake" Bentley (February 9, 1865 – December 23, 1931), born in Jericho, Vermont, is one of the first known photographers of snowflakes. He perfected a process of catching flakes on black velvet in such a way that their images could be captured before they either melted or sublimated."

All Bentley snowflake photographs are in the public domain, and can be found on numerous websites. For more information please see: Wilson Bentley on Wikipedia.

Here we see the use of striking hexagonal imagery in the emblem of the Galactic Empire, proving that hexagons can be used for "evil" purposes by those who understand the subtle nuances of the Dark Side. Consider that the emblem of the Republic is a somewhat similar figure but with eight sides instead of six. It could very well be that this use of a weaker, less aesthetically pleasing symmetry is exactly what led to the latter's downfall in the first place. The Sith no doubt knew all along that a society based on octagonality would ultimately collapse before a more hexagonal alternative.

In this screenshot of the Treaty of Armens from the TNG episode The Ensigns of Command, we see the Sheliak version of the treaty alongside the "English" (or if you will "Federation Standard") version. Note that the Sheliak, who apparently consider themselves intellectually superior to humanoids, seem to have developed some sort of flowing-hexagon-based communication system. This is probably why they consider themselves superior. If the settlers of Tau Cygna V had developed a similarly hexagonal way of life, one can only imagine how things could've worked out differently for them.

This is a screenshot of media owned by Paramount Pictures, and its use here constitutes fair use under United States copyright law. As I see it. FTVW.

I have been completely unable to find any sort of followup to this since 2003. The whole idea may have been discarded by now, I'm not sure, but considering that Plato speculated—for no particular reason modern science is aware of—that the universe was shaped like a dodecahedron nigh doz. 1,500 years ago, this is obviously a significant conjecture to put forward.

While the other four platonic solids have traditionally been associated with the four classical elements, the dodecahedron has been identified with the universe, or the aether. Did the ancients have some insight into the cosmological structure of our universe that we are only rediscovering now? Maybe! Or maybe the whole idea is crap. Who knows! But the hexagonal implications are obvious—twelve being a multiple of six, the twelve faces of the dodecahedron forming six symmetrical pairs, et cetera.