NOTE: I have transcribed and edited this from various ancient translations of Euclid, augmented and tempered where necessary by at least the structure of more modern versions. I am pretty sure there are no errors in it. This is of course only one of many interesting Euclidean propositions involving hexagons, and for anyone reading this who does not in fact own a copy of Euclid I highly recommend purchasing one right now. Thank you.
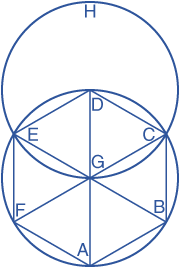 Let ABCDEF be the given circle. It is required to inscribe an equilateral and equiangular hexagon in the circle ABCDEF.
Let ABCDEF be the given circle. It is required to inscribe an equilateral and equiangular hexagon in the circle ABCDEF.
Find the center G of the circle ABCDEF, and draw the diameter AGD; and from D as a center, at the distance DG, describe the circle EGCH. Join EG and CG, and carry them through them to the points B and F. Join AB, BC, CD, DE, EF, and FA.
I say that the the hexagon ABCDEF is equilateral and equiangular.
For, since the point G is the center of the circle ABCDEF, GE equals GD.
Since the point D is the center of the circle GCH, DE equals DG
Wherefore GE is equal to GD, therefore GE also equals ED Therefore the triangle EGD is equilateral, and therefore its three angles EGD, GDE, DEG are are equal to one another, because the angles at the base of an isosceles triangle are equal.
And the sum of the three angles of the triangle equals two right angles, therefore the angle EGD is the third part of two right angles.
In the same manner, it may be demonstrated that the angle DGC is also the third part of two right angles.
And, since the straight line CG standing on EB makes the sum of the adjacent angles EGC and CGB equal to two right angles, therefore the remaining angle CGB is the third part of two right angles.
Therefore the angles EGD, DGC, and CGB are equal to one another. And to these are equal the vertical opposite angles BGA, AGF, and FGE.
Therefore the six angles EGD, DGC, CGB, BGA, AGF, and FGE are equal to one another.
But equal angles at the center stand upon equal circumferences, therefore the six circumferences AB, BC, CD, DE, EF, and FA are equal to one another.
And equal circumferences are subtended by equal straight lines; therefore the six straight lines are equal to one another, and the hexagon ABCDEF is equilateral.
I say next that it is equiangular.
For, since the circumference AF equals the circumference ED, to each of these add the circumference ABCD, therefore the whole circumference FABCD equals to the whole EDCBA.
And the angle FED stands upon the circumference FABCD, and the angle AFE upon the circumference EDCBA; therefore the angle AFE equals DEF.
In the same manner, it may be demonstrated that the other angles of the hexagon ABCDEF are each of them equal to the angles AFE and FED
Therefore the hexagon is equiangular. It is also equilateral, as was shown, and it is inscribed in the given circle ABCDEF.
Quod erat faciendum.
Corollary: From this it is manifest that the side of the hexagon is equal to the radius of the circle.
And if through the points A, B, C, D, E, and F there be drawn straight lines touching the circle, an equilateral and equiangular hexagon shall be described about it, which may be demonstrated from what has been said of the pentagon. And further, a circle may be inscribed in a given equilateral and equiangular hexagon and circumscribed about it, by a method like that used for the pentagon.
FTVW.
 Euclid IV.15: To inscribe a regular hexagon in a given circle
Euclid IV.15: To inscribe a regular hexagon in a given circle