The permutohedron

We seem to have fallen a bit behind in terms of keeping this site updated with RELEVANT MATHEMATICAL INFORMATION about hexagons. This is a deficit we're looking to correct as soon as possible. First up, let us consider the permutohedra. We at HEXNET.ORG have been meaning to write something about permutohedra for a couple of years now, but have never really found a good opportunity to so. WE WILL NOT EXPEND GREAT EFFORT DOING SO NOW. It will suffice to merely describe the concept in conjunction with some helpful imagery, which will hopefully serve as a useful foundation for further geometrical observations and investigations in the near future.

Please note: part of the reason we've postponed writing about permutohedra is actually our continuing inability to effectively create 3D images. This is too important a matter to tolerate further delays though, so we've decided to just rip off the appropriate material from Wikipedia and move on.

Talk of permutohedra in the popular media skyrocketed last year—due indirectly to my actions it seems—when they were mentioned in a brief writeup associated with Super Hexagon (another item we should really get around to writing about one of these days). Unfortunately, this writeup gave the erroneous impression that hexagons are first-order permutohedra, when in fact they are third-order permutohedra. A first-order permutohedron is just a dot on a line, and is in any event not a particularly good example of the permutohedral class as a whole. We hope that this post may go some way towards correcting this recent misperception.

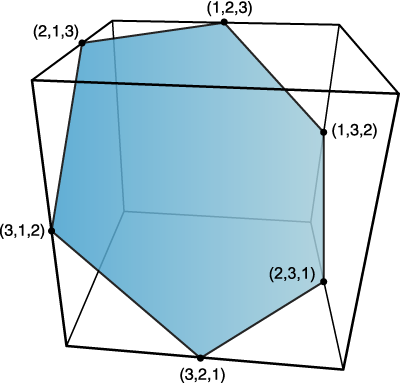
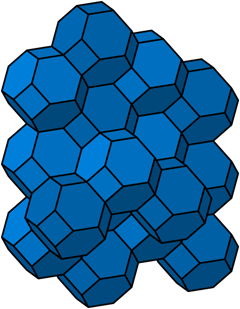
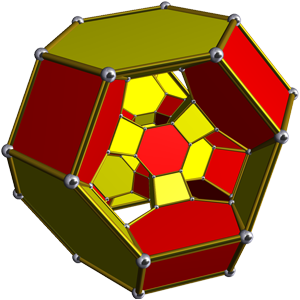
To that end: The permutohedron of order n is the n-1 dimensional polytope embedded in an n-dimensional space, the vertices of which are formed by permuting the coordinates of the vector (1, 2, 3, ..., n). Thus, the first-order permutohedron is a vertex at coordinate 1 on a line (though this is again a somewhat degenerate case); the second-order permutohedron is a line segment formed between coordinates 1,2 and 2,1; and the third-order permutohedron, our beloved hexagon, can be visualized as a hexagon bisecting a cube spanning two units between coordinates 1 and 3 (if the diagram of the hexagon above was consistent with the diagram of the second-order permutohedron, it would include the 0,0,0 origin of the embedding space, which lies one further unit cube beyond the far vertex perpendicular to the plane of the hexagon). The truncated octahedron represents the fourth-order permutohedron, embedded in 4-space, and the omnitruncated 5-cell (or 4-simplex) represents the fifth-order permutohedron in 5-space, etc.

As a consequence of this, all permutohedra lie entirely in the hyperplanes of their embedding spaces consisting of all points whose coordinates sum to the number 1 + 2 + ... + n. In the case of the hexagon, not only do the coordinates 1, 2, and 3 add up to 6 at the vertices, but the coordinates of every other point on the plane of the hexagon also add up to 6. All such hyperplanes can be tiled with translated copies of their respective permutohedra. As hexagons tessellate the plane, so truncated octahedra tessellate 3-space, the omnitruncated 5-cell tessellates 4-space, etc. One can visualize this most easily with the second-order permutohedron pictured above, where the next line segment on the upper left would be defined by the additional vertex at 0,3, the next one beyond that would be -1,4, etc.

All permutohedra of order > 3 contain hexagonal 2-faces—indeed, all 2-faces in higher-order permutohedra are either hexagons or squares, and all 3-faces are truncated octahedra, hexagonal prisms, or cubes. It goes without saying, of course, that no permutohedra of order > 3 are regular polytopes.

Permutohedra do not seem to be particularly widely discussed in the mathematical literature, evidently because they are seen as rather trivial and unimportant—they are perhaps a somewhat interesting way of representing certain combinatorial relationships, etc., but beyond that they don't really do much per se. This is perhaps true as far as it goes (though some would say the same thing about hexagons themselves believe it or not), but they do nonetheless have several other interesting properties worth noting, particularly in the context of their potential hexagonal import:

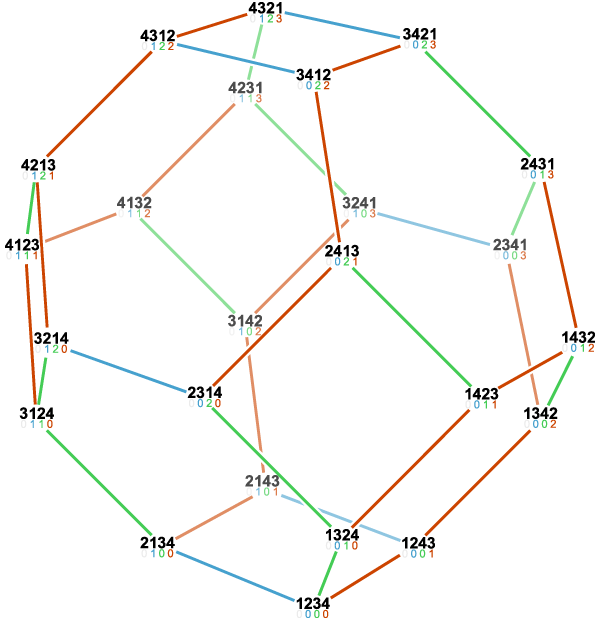
The n-order permutohedron has of course n! (the factorial of n) vertices: 1 = 1 vertex, 1x2 = 2 vertices, 1x2x3 = 6 vertices, 1x2x3x4 = 24 vertices, etc. Somewhat less obviously perhaps (and here I'm just going to quote Wikipedia verbatim), each permutohedron has one facet for each nonempty proper subset S of {1, 2, 3, ...,n}, consisting of the vertices in which all coordinates in positions in S are smaller than all coordinates in positions not in S. Thus, the total number of facets is 2n–2. More generally, the faces of the permutohedron (including the permutohedron itself, but not including the empty set) are in 1:1 correspondence with the strict weak orderings on a set of n items: a face of dimension d corresponds to a strict weak ordering in which there are n–d equivalence classes. Because of this correspondence, the number of faces is given by the ordered Bell numbers. Thus, the total number of faces (that is, the total number of vertices, edges, polygonal faces, polyhedral cells, etc., up to and including the permutohedron itself) proceeds in the sequence 1 = 1, 2 + 1 = 3, 6 + 6 + 1 = 13, 24 + 36 + 14 + 1 = 75, 120 + 240 + 150 + 30 + 1 = 541, etc.

All permutohedra are the omnitruncated simplices of their respective dimensionality (that is, the n-1 dimension). Which, as far as I understand it, essentially involves turning all the faces of a simplex (that is, a generalized, higher-dimensional triangle) into outer facets. Most obviously, the hexagon can of course be construed as a triangle with three smaller removed from its corners—transforming its 3 edges and 3 vertices into 6 facets. The same is true of the truncated octahedron, which turns the 4 faces, 6 edges, and 4 vertices of a tetrehedron into 14 facets. And likewise up through the great chain of permutohedrality.

In summary then, the concept of permutohedrality gives us I think an important geometrical framework with which to understand some of the more important and unique properties of the hexagon. Indeed, one thing that all summaries of the permutohedral concept seem to mention is that they are n-dimensional generalizations of the hexagon. (It was such language that first brought them to our attention some years back.) This is of course true to a large extent, and the analogue with hexagonal principles certainly must be a part of any comprehensive account of the concept, but it should be remembered that the permutohedral lineage is but one of several unique and interesting categories that encompass the noble hexagon. One can certainly argue, I think with a great deal of justification, that the concept of permutohedrality encompasses the nucleus of hexagonal exceptionalism—in particular, by generalizing the deep relationship between hexagons and the three orthogonal Cartesian dimensions of Euclidean space, and by extension the relationship between the sixfold nature of the hexagon and the ontological procession from the monad to the dyad to the triad. But conversely—at least in the context of geometry—one might make the same claim about the vector equilibrium, or if you will cuboctahedron—which embodies the hexagonal virtue of having a vertex radius equal to its edge length (the hexagon and vector equilibrium being the only regularish polytopes in their respective spaces with this property), which in turn speaks to the relationship between circle packing and hexagonal tessellation, and about which we will have more to say in the future. Even the tedious cube must be said to have some claim to the hexagonal legacy—though certainly less so than either the truncated octahedron (which really should have a better name) or the vector equilibrium. At any rate, the point is worth emphasizing yet again that what makes the hexagon truly exceptional and superlative above all other shapes, in all possible spaces, is not that it is merely the planar representation of a certain class or category of thing, but that it represents the confluence and nexus of many categories—indeed, perhaps of all ontologically significant categories. It is this confluence that is the essence of hexagonal superiority, and it is this that must be exalted above all other properties.

All four main images here are slightly edited versions of images available on Wikimedia, as noted. All images include captions linking back to their original media files. The first and second images, of the second- and third-order permutohedra, are the work of Wikimedia user R. A. Nonenmacher, and are licensed under the Creative Commons Attribution-Share Alike 3.0 Unported, 2.5 Generic, 2.0 Generic, and 1.0 Generic license. The third image, of the truncated octahedron, is by Wikimedia user Lipedia and has been released into the public domain. The fourth image, of the omnitruncated 5-cell, is by Wikipedia user Claudio Rocchini and is licensed under the Creative Commons Attribution 3.0 Unported license. The solid projection of the omnitruncated 5-cell in the body of the post can be found here, and was created by Robert Webb with Mr. Webb's Stella software. All other images used here have been released into the public domain as well, and we thank those who have done so.