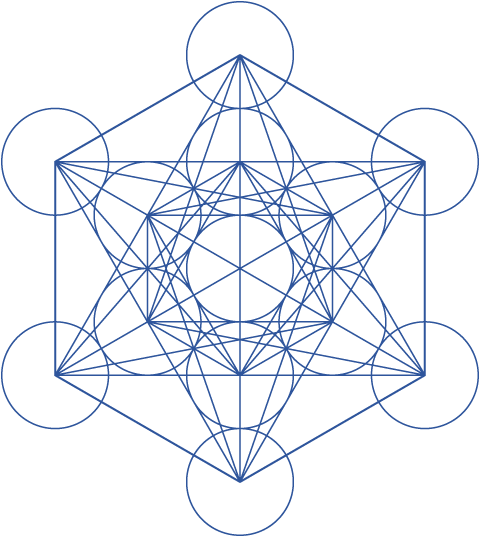
Metatron's Cube
Metatron is an angel described in Jewish and other Abrahamic religious texts, variously identified as the Scribe of God, the Lesser Tetragrammaton, et cetera. He/it is closely identified with the prophet Enoch, and by many accounts they are one and the same entity.
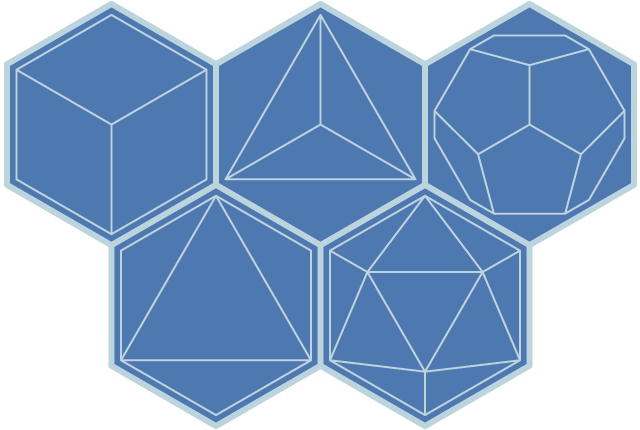
The cube itself consists of thirteen (doz. 11) circles, six of which emanate out from seven hexagonally packed circles in the center, with line segments connecting the center of each circle with the center of every other circle. This has the effect of producing a highly hexagonal pattern onto which one can map orthographic projections of all five Platonic solids. Note that this figure can also be expressed in the form of an actual cube, which sixteen (doz. 14) spheres instead of thirteen circles.