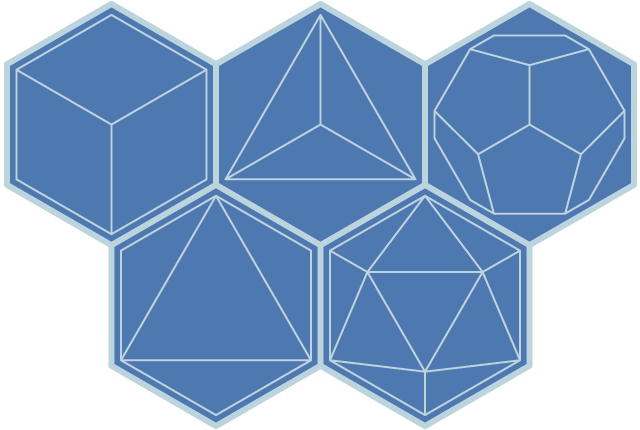
In this diagram we see that four of the five platonic solids can be projected in two dimensions as hexagonally-symmetric figures. The hexahedron, octahedron, and icosahedron can all be orthographically projected as regular hexagons, and the dodecahedron can be so projected as a somewhat lopsided yet equal-angled hexagon (not shown), or as a hexagonally-symmetrical dodecagon (shown here). The tetrahedron—or "freak" polyhedron if you will—can of course be projected as an equilateral triangle, which although not truly hexagonal is still of the same general angular family.
Note well that although the hexahedron and octahedron can obviously be projected as squares and the icosahedron can be projected as a regular decagon, only the hexagon uniquely corresponds to the symmetries of all five platonic solids—and, by extension, their various semiregular archimedean counterparts and so on—when projected in two dimensions. This is related to the fact that all five platonics have either three-sided faces or three-way vertices, and can easily be centerered on these triangularly-symmetric elements. In addition, it is interesting to remember that the three familiar dimensions of cartesian space can themselves be projected as a sort of hexagonally-symmetric arrangement of vectors—as we see, in a sense, in the projection of the cube.
 Hexagonal projection of the platonic solids
Hexagonal projection of the platonic solids