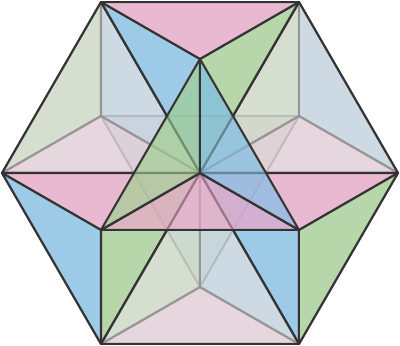
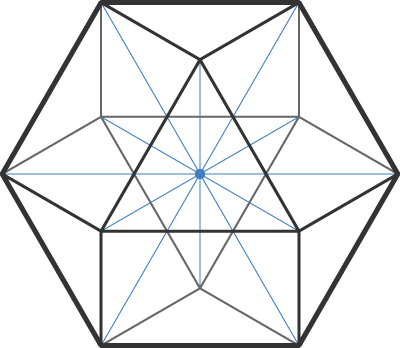


Here we see the illustrious cuboctahedron, or vector equilibrium. Along with the truncated octahedron, it can be considered, in some sense, a three-dimensional analogue to the hexagon. Though it has no hexagonal faces, the cuboctahedron can be seen to consist of four hexagonal rings or planes arranged in the manner of tetrahedral symmetry. That is, if one took a tetrahedron, replaced its four faces with hexagons (as for instance with a truncated tetrahedron), and collapsed all four hexagonal sides so that they all shared a common center, the vertices of the hexagons would describe a cuboctahedron, with each vertex shared between two intersecting hexagons, collapsing the original 24 vertices of the four hexagons into the 12 vertices of the cuboctahedron. (Likewise, of course, the cuboctahedron can simply be seen as a sort of "expanded" tetrahedron, with four of its eight triangular faces representing the original four faces of an inner tetrahedron, the remaining four triangles representing its four vertices, and the square faces representing its edges.) Tetrahedral symmetry being the simplest type of polyhedral symmetry, and the only one suited to this sort of fitting together of hexagonal planes, the cuboctahedron represents a unique extension of and analogue to hexagonal symmetry in three dimensions.
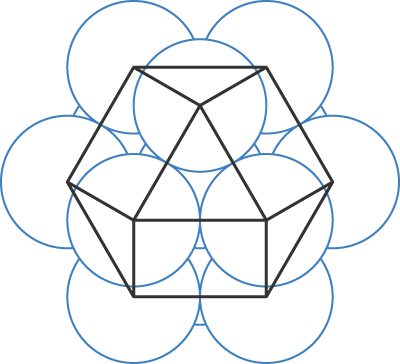
From the idea of the cuboctahedron as four intersecting hexagonal planes, it follows that, like the hexagon, the radius between the center of the cuboctahedron and its vertices is equal to the length of its edges. As with the hexagon in 2-space, the cuboctahedron is the only uniform convex polyhedron with this quality. Likewise, as hexagons can be subdivided into equilateral triangles, so the cuboctahedron can be seen to consist of six half-octahedra and eight tetrahedra clustered around the center, forming the vertex figure of the tetrahedral-octahedral tessellation. Pairing the half-octahedra with their remaining halves, and continuing the same arrangement of edge-sharing tetrahedra around these octahedral "cavities," this pattern of tetrahedral-octahedral tessellation can be continued outward indefinitely, with identical cuboctahedral symmetry radiating from every vertex in the resulting tessellation. Despite this, however—and unlike the truncated octahedron—the cuboctahedron cannot by itself tessellate space; when only cuboctahedral units are fit together, one will always be left with either space left over, or overlapping tetrahedral/half-octahedral cells.
The face-centered cubic arrangement of close-packed spheres (which, as we've described elsewhere, is arguably more hexagonal than the so-called "hexagonal close packing" arrangement) is essentially identical to this tetrahedral-octahedral tessellation. Thus, a sphere placed at the center of a cuboctahedron with a diameter equal to the edge length of the latter can be surrounded by twelve neighboring spheres of equal size, each arranged at one of the vertices of the cuboctahedron. This, again, can be expanded outward indefinitely, though the particular unit of spheres in this configuration will not fill such a packing arrangement by itself.
The dual of the cuboctahedron is the delightfully quirky rhombic dodecahedron, which can, in fact, tessellate space by itself, in the manner of FCC-packed spheres. That is, if spheres in a face-centered cubic packing were expanded until they filled all available space, or the vertices of a tetrahedral-octahedral tessellation were themselves turned into spheres and so expanded, they would become rhombic dodecahedra.
At this point you may be wondering "But wait, what about hexagonal close packed spheres? They, too, have twelve neighboring elements. Is there a cuboctahedron-like polyhedron that represents their packing arrangement?" And of course there is: the somewhat absurd triangular orthobicupola, and its dual, the quite possibly more absurd trapezo-rhombi dodecahedron. A moment's reflection on these shapes and their obvious contrast with the cuboctahedron and its extended family of tetrahedral-octahedral symmetries should make it somewhat self-evident why I consider FCC, and not HCP, to be the true successor to hexagonal symmetry in three dimensions. (I can only assume "hexagonal close packing" was named by someone with only the most superficial appreciation of hexagons, and who presumably didn't think very highly of them.)
The cuboctahedron, broadly for the reasons touched on above, was of particular interest to Buckminster Fuller, who rebranded it as the "vector equilibrium." (Drawing particular attention to the equivalence between radius and edge length, and its role in the tetrahedral-octahedral tessellation.) I have used both terms on this site and elsewhere, though of late I've gravitated back towards "cuboctahedron," due to its syllabic parsimony, widespread acceptance, etc. It should be remembered however that Fuller himself was largely responsible for popularizing the tetrahedral-octahedral space frame truss in the middle and late 20th century, and that it is this accomplishment, along with his broader Synergetics work with octahedral/tetrahedral symmetry, that represents Fuller's most significant and lasting contribution to the hexagonal arts and sciences—far moreso than his work with the somewhat superficially hexagonal (though still of course important) geodesic dome, for which he is perhaps more popularly remembered. Indeed, thanks to the important work of Fuller and others in incorporating these tetrahedral/octahedral symmetries into the language of modern design and architecture, it is truly through the cuboctahedron, above all other uniform polyhedra, that we have come to see the tangible physical impact of hexagonal thinking in the modern world, giving us some hint of the promise it holds for our future and for our hexagonal destiny.
 The cuboctahedron
The cuboctahedron
I'm shocked, just shocked, that there is no mention of the fact that the edges of the cuboctahedron form four regular hexagons around the center, each tilted at a congruent angle from another.
I suppose I've spent so much time thinking about cuboctahedra that I just assumed this was implicitly understood by everyone. But you're right, it should be at least mentioned. (Particularly given the naive tendency of some to judge the relative hexagonal import of a polytope solely by the number of hexagonal faces it may or may not have.)
I'll look into adding something about it, and hopefully about its larger import to the relationship between tetrahedral symmetry and hexagonal principles, etc. Thanks.
I've significantly modified this post, including the addition of a NEW IMAGE. It's a bit more rambling now, but hopefully also has a bit more of a thematic flow, and touches on all the important issues at hand.