Here we see illustrated the the principle that, for any given natural number n, the sum of the first n centered hexagonal numbers is equal to the cube of n. In this particular example, 1+7+19+37=4^2=64. In the color scheme above, the first hex number corresponds to the blue cube on the vertex of the cube figure, while the seven cubes of second hex number represent the purple shell of cubes behind this, and so on—one can easily visualize how the number of units in any particular hex number correspond to the equivalent shell of cubes.
This matter is also addressed in our feature-length educational video, "A series of cubes" (using the same graphics no less).
(Note that in any given shell layer beyond the first corner cube, there are "hidden" cubes in the center and along the edges that cannot be seen from this perspective.)
 Cubic sums of centered hexagonal numbers
Cubic sums of centered hexagonal numbers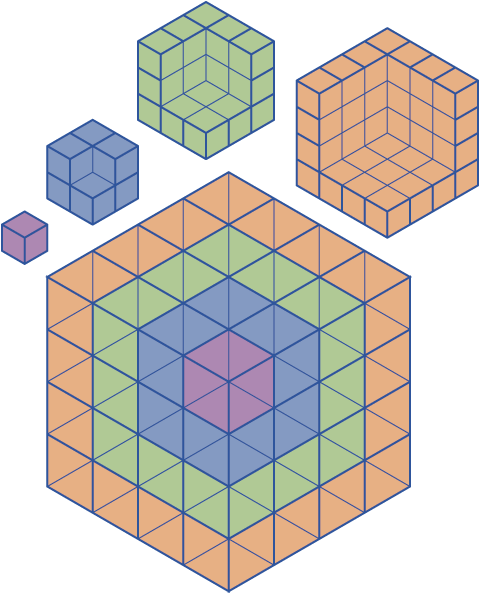
This explanation shows the shells being built up very nicely (and even better if you look at the video). The downside is that there are some hidden blocks.
I took an alternative approach in my own visualization and built the shells from the outside in so that all blocks are always visible.
The downside of my visualization is that the shells aren't as easy to explain.
I also provide an algebraic proof on my blog.
Yes that is why I linked to your post from my HEXAGONS page - it is I think a bit clearer on the first pass than my cryptic cube shells. I am not particularly proficient in the whole 3D modeling thing though, mostly because I find the orthogonal coordinate system oppressive. I am glad someone bothered to make a better demonstration.
Thanks for stopping by!