Contents
- Introduction
- Some observations about hexagons
- The basic geometry of hexagons
- Hexagonal tessellation
- Hexagons and circles
- Hexagons and triangles
- Conclusion
Introduction
 The following is a brief survey of some elemental properties of hexagons, and why they might be useful. It is not intended to be a comprehensive treatment of the subject. My specific concern here is with the mathematical properties of hexagons, and, to an extent, their role in the natural world. I have avoided discussing hexagons as they pertain to human culture, religion, history, and other "local" concerns, though there are many fascinating instances of hexagonality and sixness in these areas, and they will no doubt be treated more fully elsewhere at another time.
The following is a brief survey of some elemental properties of hexagons, and why they might be useful. It is not intended to be a comprehensive treatment of the subject. My specific concern here is with the mathematical properties of hexagons, and, to an extent, their role in the natural world. I have avoided discussing hexagons as they pertain to human culture, religion, history, and other "local" concerns, though there are many fascinating instances of hexagonality and sixness in these areas, and they will no doubt be treated more fully elsewhere at another time.
This article is very much a work in progress, and is not really "done" in any meaningful sense. It is current as of its last update. I intend to replace or at least supplement it with a more comprehensive and eloquent survey of hexagonal concepts at some point. Bear in mind that only a very small fraction of the interesting properties of hexagons are explored in this article, and it is hoped that a more complete view of their qualities will emerge through the sum of diverse material available on this site.
A note about terminology: As is my general custom, and unless otherwise noted, "hexagon" refers to regular hexagons only. In addition, I tend to speak rather loosely about "hexagonal" this and that. When describing things as "hexagonal" I am often referring in a very broad sense to all hexagonal and hexagon-like symmetries, and not necessarily to regular hexagons per se.
Some observations about hexagons
A hexagon is a closed plane figure with six edges and six vertices. A regular hexagon is a convex figure with sides of the same length, and internal angles of 120 degrees. It has six rotational symmetries and six reflection symmetries, making up the dihedral group D6.
The properties of hexagons are numerous and interesting. At first glance, several facts about them stand out:
- Hexagons are one of only three regular polygons to tessellate the Euclidean plane (along with squares and triangles).
- The hexagonal tessellation is combinatorially identical to the close packing of circles on a plane.
- Hexagons are the only regular polygon that can be subdivided into another regular polygon. (As far as I know, hexagons are the only regular polytope of any dimension with this particular property.)
- In a related fact, hexagons are the unique regular polygon such that the distance between the center and each vertex is equal to the length of each side (sharing this property with the cuboctahedron in 3-space).
- Hexagons are the first polygons—when ascending by number of sides—that do not form the faces of a regular convex polyhedron in Euclidean space. The three polygons with fewer sides compose the surfaces of the five platonic solids, but no polygon with six or more sides can be employed for this purpose. A consequence of this is that no regular polytope, in any dimension, has hexagonal faces—though many have hexagon-like or hexagonally-symmetric vertices or other elements.
- Hexagons are third-order permutohedra, meaning each vertex of a hexagon can be described with Cartesian coordinates using one of six permutations of the numbers 1, 2, and 3. Such a hexagon would lie on a plane consisting of all points with coordinates that add up to 6, and would bisect a cube of unit length 2 between coordinates 1 and 3.
 Another interesting thing about hexagons—and perhaps the most striking fact about them—is that they do, in fact, have six sides. Let us then take a moment to enumerate some interesting facts about the number six:
Another interesting thing about hexagons—and perhaps the most striking fact about them—is that they do, in fact, have six sides. Let us then take a moment to enumerate some interesting facts about the number six:
- Six is a highly composite number, the second-smallest composite number, and the first perfect number. That is, 1*2*3 = 1+2+3 = 6.
- In a related matter, six is the only number that is both the sum and the product of three consecutive natural numbers (1, 2, and 3).
- Six is the smallest composite squarefree integer, and by extension, the first natural number with two distinct prime factors (2 and 3).
- Cubes have six sides, and they are pretty useful too.
And so on. It is evident that most of the unique and interesting properties of six ultimately derive from the fact that it is the product and sum of the first three natural numbers, and that, in a more philosophical sense, it can been seen as combining the archetypal values of unity, duality, and trinity into a somewhat balanced whole. The unity divides into duality, which is reconciled in the trinity (one plus two, or two combining into one), which is then recombined with duality and unity—either additively or multiplicatively—to produce our esteemed six.
Of course, there are many other hexagonal and hexagonally-pertinent numbers, and it would be a mistake to only associate hexagonality with six. Seven, for instance, has often featured prominently in human culture, and in certain religious traditions in particular. If one goes back and looks at the various geometrical forms associated with such sevens, it is often apparent that they are construed to form six peripheral entities around one central entity—in the fashion of hexagonally packed circles, or hexagonal tessellation. Seemingly non-hexagonal numbers such as eight and ten also hexagonal connotations, as do the various centered hexagonal numbers, regular hexagonal numbers, et cetera. To say nothing of multiples of six, such as twelve, which is also a truly great number in and of itself (adding divisibility by 4 to the 1, 2, 3 situation). But certainly it goes without saying that six has a distinct connection to hexagonality, and it is worth being aware of its unique and interesting properties in this respect.
It is ultimately my contention that, the more you look into the mathematical and physical underpinnings of the universe, the more prominent and interesting hexagons, sixes, and their various analogues in other mathematical systems become. It is beyond the scope of this article to posit any sort of overarching interpretation of this, but it is something worth noting and accounting for in our interpretations of, and relationships with, reality.
At this point I would like to expand on several of the hexagonal matters raised above.
The basic geometry of hexagons
Let us first take a moment to look more closely at the basic proportions and ratios of the noble hexagon:
 The apothem of a regular hexagon is equal to half the square root of 3. This can be demonstrated with a unit hexagon, where each side is given the length of 1. We can then draw a right triangle using the vertex-to-vertex diameter of the hexagon as a hypotenuse. Since the diameter of such a hexagon is known to be 2, we are left with one undefined edge of our triangle, equal the distance between two opposing edges of the hexagon (which is twice the apothem). Let us call this edge x. The Pythagorean theorem then tells us that 12+x2 = 22. It then follows that 1 + x2 = 4, x2 = 3, and thus x = √3. Therefore the "height" to "width" of a regular hexagon is equal to √3/2. Quod erat demonstrandum.
The apothem of a regular hexagon is equal to half the square root of 3. This can be demonstrated with a unit hexagon, where each side is given the length of 1. We can then draw a right triangle using the vertex-to-vertex diameter of the hexagon as a hypotenuse. Since the diameter of such a hexagon is known to be 2, we are left with one undefined edge of our triangle, equal the distance between two opposing edges of the hexagon (which is twice the apothem). Let us call this edge x. The Pythagorean theorem then tells us that 12+x2 = 22. It then follows that 1 + x2 = 4, x2 = 3, and thus x = √3. Therefore the "height" to "width" of a regular hexagon is equal to √3/2. Quod erat demonstrandum.
An interesting consequence of this is that regular hexagons and equilateral triangles have exactly the same ratio of "width" to "height." That is, the minimum diameter of either a hexagon and a triangle is √3/2 its maximum diameter. Indeed, √3 is a recurring value throughout triangular and hexagonal geometry—for instance, the diagonal distance between two opposing vertices of a cube also equals √3 (compare to the diagonal width of a square, which is √2, for reasons similar to those outlined above). As a consequence, of course, √3 features prominently in plane trigonometry, where it is prominent in the expression of various 60 and 30 degree values.
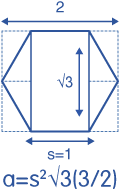 The area of a hexagon can likewise be calculated with √3. Let us first define the edge length of our hexagon as s. We can then draw a rectangle between two opposing edges of the hexagon with the area s2√3. If we then consider that the we have 4 right triangular sections left over, and that the hexagon itself can be considered to consist of 12 such triangles, 8 of which we have incorporated into our rectangle, it is clear that the total area of the hexagon is one and a half times the area of the rectangle. Thus, s2√3(3/2). Quod erat faciendum.
The area of a hexagon can likewise be calculated with √3. Let us first define the edge length of our hexagon as s. We can then draw a rectangle between two opposing edges of the hexagon with the area s2√3. If we then consider that the we have 4 right triangular sections left over, and that the hexagon itself can be considered to consist of 12 such triangles, 8 of which we have incorporated into our rectangle, it is clear that the total area of the hexagon is one and a half times the area of the rectangle. Thus, s2√3(3/2). Quod erat faciendum.
(This is also an example of the more general principle that the area of a regular convex polygon is equal to the product of the perimeter and the apothem divided by 2 (in this case, 6s√3/2/2). This is due to the fact that we can divide an n-sided regular convex polygon into 2n right triangles, by drawing line segments from the center to each vertex as well as from the center to the middle of each edge. We can then suppose that each 2 right triangles thus formed can be combined to form a rectangle with the area of the apothem multiplied by half the edge length. Thus, by simply dividing the product of the apothem and the total perimeter in half, we arrive at the total area of the polygon.)
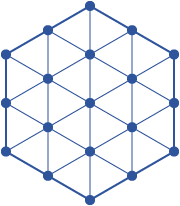
Hexagonal tessellation
 As previously noted, hexagons can be tiled or tessellated in a regular pattern on a flat two-dimensional plane. That is, a hexagon can be bordered by six other hexagons, which can themselves be bordered by six hexagons (including each other), and so on, indefinitely in any direction, with no empty space left over. Note that although there are any number of potential tilings consisting of two or more types of polygons, only hexagons, squares, and triangles can form such regular tilings by themselves. (Likewise, in three dimensions, among uniform polyhedra, only the six-sided cube and the hexagonally-analogous truncated octahedron can form space-filling tessellations by themselves.)
As previously noted, hexagons can be tiled or tessellated in a regular pattern on a flat two-dimensional plane. That is, a hexagon can be bordered by six other hexagons, which can themselves be bordered by six hexagons (including each other), and so on, indefinitely in any direction, with no empty space left over. Note that although there are any number of potential tilings consisting of two or more types of polygons, only hexagons, squares, and triangles can form such regular tilings by themselves. (Likewise, in three dimensions, among uniform polyhedra, only the six-sided cube and the hexagonally-analogous truncated octahedron can form space-filling tessellations by themselves.)
The hexagon is of course therefore the highest-sided tessellable regular polygon. This makes it uniquely important in a variety of fields, since it has the advantage of spacing out each constituent hexagon more or less evenly from its neighbors. That is, any given point inside a hexagon (whether in a tiling of hexagons or not) is closer to the center of that hexagon than any given point in an equal-area square or triangle would be. Since squares and triangles have more acute angles, points near their corners are further away from points elsewhere in their area than they would be at similar locations in a hexagon. Now, the same would be true for any higher-sided polygon as well—the ideal efficiency for enclosure of a given area being, ultimately, a circle. But again, hexagons have the tessellation advantage. Thus, for any task that requires both a regular grid of cells or elements, and the efficient enclosure of the area of that cell, a hexagonal tessellation is the logical and necessary choice. Common examples of this use of hexagonal cells can be found in such varied fields as cellular automata, statistical sampling, board games, computer games, the comb of the esteemed honeybee, and so on.
A related property of hexagonal tessellation is that it creates no diagonal edges. (By "diagonal" here I mean neighbors that share only a vertex border, not an edge border—I do not know of a more precise mathematical term for this, though I am aware it is not exactly what "diagonal" means in the strictest sense of the term.) If you look at tilings of triangles and squares, you will of course see that both have diagonal connections between neighboring elements at their vertices. In a square tessellation, every square connects to one square directly on each side and one square diagonally on each vertex, for eight total neighboring squares, and in a triangular tessellation every triangle connects to one triangle on each side, and three triangles diagonally on each vertex, for a total of twelve neighboring triangles. These diagonal connections are, of course, the key to the ability of squares and triangles to form regular polyhedra—by removing the diagonal neighbors from around a square, one can easily fold back the remaining neighboring squares until they join each other directly to form a cube, and by similarly removing one, two, or three diagonal neighbors from a triangle one can fold the remaining triangles into an icosahedron, octahedron, or tetrahedron, respectively. (Though it should be noted that, although both diagonally-tessellating regular polygons happen to form regular polyhedra when folded back in this way, there is, on the surface of it, no particular reason why this must be the case.) Conversely, this is why hexagons cannot form regular polyhedra of their own. Each external angle of a hexagon is 120 degrees, and the only possible vertex configuration—in Euclidean space—is with three neighboring angles totaling 360 degrees (with the exception of the "degenerate" hexagonal dihedron of course, which isn't particularly useful for our purposes here).
 Hexagonal tessellation is the dual of triangular tessellation—you can turn the former into the latter by replacing all vertices with triangles, and all hexagons with vertices. Likewise in a triangular tessellation, if you replace all triangles with vertices, and all vertices with hexagons, you are left again with a hexagonal tessellation. (Any polytope or tessellation with inverse quantities of outer elements can be reversed by the same principle: the octahedron is the inverse of the cube, and the icosahedron is the inverse of the dodecahedron—each represents the vertex/face reversal of its counterpart. This can be represented notationally by reversing a particular object's Schläfli symbol—in the case of hexagonal and triangular tessellation, changing {6,3} to {3,6}, or vice versa.) In addition, as hexagons can be divided into equilateral triangles, and equilateral triangles can be combined into hexagons, the triangular tessellation can be considered a simple subdivision of the hexagonal, or vice versa.
Hexagonal tessellation is the dual of triangular tessellation—you can turn the former into the latter by replacing all vertices with triangles, and all hexagons with vertices. Likewise in a triangular tessellation, if you replace all triangles with vertices, and all vertices with hexagons, you are left again with a hexagonal tessellation. (Any polytope or tessellation with inverse quantities of outer elements can be reversed by the same principle: the octahedron is the inverse of the cube, and the icosahedron is the inverse of the dodecahedron—each represents the vertex/face reversal of its counterpart. This can be represented notationally by reversing a particular object's Schläfli symbol—in the case of hexagonal and triangular tessellation, changing {6,3} to {3,6}, or vice versa.) In addition, as hexagons can be divided into equilateral triangles, and equilateral triangles can be combined into hexagons, the triangular tessellation can be considered a simple subdivision of the hexagonal, or vice versa.
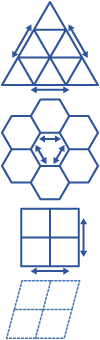 A final advantage of hexagonal tessellation or hexagonal lattices worth considering is its compressive and tensile strength and efficiency when compared to other tessellatory options. If we consider an abstract physical "structure" formed of the line segments between vertices of a regular polygonal tessellation (i.e., chicken wire), it is clear that such a structure formed into a hexagonal lattice will provide the ideal blend of efficiency and strength over similar triangular or square structures. Either a triangular or hexagonal structure built in this way will be demonstrably stronger than a square structure, and while a triangular structure, all things being equal, will be stronger than a hexagonal one, it will also use more material (with six lines connecting at every vertex instead of three) and thus be less "efficient"—though for particularly applications obviously it may be preferable.
A final advantage of hexagonal tessellation or hexagonal lattices worth considering is its compressive and tensile strength and efficiency when compared to other tessellatory options. If we consider an abstract physical "structure" formed of the line segments between vertices of a regular polygonal tessellation (i.e., chicken wire), it is clear that such a structure formed into a hexagonal lattice will provide the ideal blend of efficiency and strength over similar triangular or square structures. Either a triangular or hexagonal structure built in this way will be demonstrably stronger than a square structure, and while a triangular structure, all things being equal, will be stronger than a hexagonal one, it will also use more material (with six lines connecting at every vertex instead of three) and thus be less "efficient"—though for particularly applications obviously it may be preferable.
The fact that square lattices do not share the strength of hexagonal or triangular lattices becomes obvious when one examines an illustration of the three structures, imagining that at each vertex the line segments of the structure are pushing together or pulling apart with the force they would in a physical structure. It is clear that, with four segments extending out at exact 90 degree angles at each vertex, the square structure easily shears either horizontally or vertically—it has no other angles supporting its structure, so they just sort of flop around. Conversely, in the triangular and hexagonal configuration, line segments converging at 60 and 120 degree angles prevent any shearing or collapsing—they balance each other out and distribute the load (whatever it may be) evenly.
For instance, if you imagine a hexagonal or triangular lattice "holding up" an object, it is clear that the alternating angles of the hexagonal and triangular lattices would do more to distribute weight to the lower levels than the orthogonally-confined square lattice would. The same principle easily applies to force distribution applications in three dimensions as well—such as we see, for instance, in the remarkable tensile strength of carbon nanotubes, in the distribution of weight by geodesic domes, et cetera.
Hexagons and circles
The hexagonal packing arrangement is the most efficient system for packing circles on a flat plane. That is, as with hexagonal tiling, you can place six neighboring circles of the same size around a circle, and six circles around each of them, and on so in indefinitely, such that the arrangement of circles is identical to the arrangement of hexagons in a hexagonal tessellation. Put another way, one can inscribe circles in every hexagon in a hexagonal tessellation, remove the hexagons, and one will be left with perfectly close-packed circles. This is useful and interesting for a number of reasons, such as that it allows hexagonally packed circles to be easily modeled with hexagons or triangles when necessary.
 An interesting phenomenon related to this intersection between circular and hexagonal geometry is that hexagonal patterns often appear spontaneously when natural forces are trying to approximate circles. (This is no doubt a large part of the reason why hexagons are generally considered a very "natural" shape.) For instance, convection cells often form into hexagons. Since each cell naturally tends towards the most efficient enclosure of its space, they tend towards circularity, but since each cell has any number of neighboring cells pressing up against it, the result is a quasi-hexagonal tiling of sorts. A pertinent example of this would be the Giant's Causeway in occupied Ireland: When the basaltic lava that formed the structure was initially cooling, it contracted into roughly cylindrical cells. As the cells cooled into solid rock, they naturally took on the hexagonal geometry of packed circles.
An interesting phenomenon related to this intersection between circular and hexagonal geometry is that hexagonal patterns often appear spontaneously when natural forces are trying to approximate circles. (This is no doubt a large part of the reason why hexagons are generally considered a very "natural" shape.) For instance, convection cells often form into hexagons. Since each cell naturally tends towards the most efficient enclosure of its space, they tend towards circularity, but since each cell has any number of neighboring cells pressing up against it, the result is a quasi-hexagonal tiling of sorts. A pertinent example of this would be the Giant's Causeway in occupied Ireland: When the basaltic lava that formed the structure was initially cooling, it contracted into roughly cylindrical cells. As the cells cooled into solid rock, they naturally took on the hexagonal geometry of packed circles.
It is also worth noting that hexagons play a significant role in the three-dimensional close-packing spheres, in both the hexagonal close packing and face-centered cubic systems. Both HCP and FCC are composed of "sheets" of hexagonally-packed spheres—they differ only in how the sheets are stacked together. It should be noted that, despite their respective names, an argument can be made that face-centered cubic packing is actually more "hexagonal" than the so-called hexagonal packing—the latter getting its name more from an absence of cubicality than from a preponderance of hexagonality. Note that both HCP and FCC are vastly less efficient than hexagonal packing is in two dimensions—the former have a density of π/(3√2), while the latter has a density of π/√12. The regular close-packings of n-spheres up to 8 dimensions are also known, evidently, and may or may not involve hexagonal or hyperhexagonal topologies.
Hexagons and triangles
In many ways, the relationship between triangles and hexagons is a continuation of the relationship between hexagons and circles. I consider them part of one unbroken geometrical continuum (rooted in the rather obvious fact, I suppose, that the closest arrangement of three equal-sized circles is at the vertices of an equilateral triangle with an edge length equal to the diameter of the circles). But for the moment, let us look specifically at the relationship between triangles and hexagons:
As already noted, a regular hexagon can be subdivided into six equilateral triangles. The hexagon and the triangle are the only two regular polygons, and I believe the only two regular polytopes, to share this property. In addition to the hexagon being divisible into equilateral triangles, the triangle is of course itself divisible into subtriangles, and since the grouping of any six triangles arranged around a vertex produces a hexagon, triangles can divided into hexagons as well, although with triangular spaces left over. A triangle subdivided into 9 subtriangles can be construed as a hexagon with three equilateral triangles formed by extending the edges of alternating sides of the hexagon until they meet (such as in the figure of the Tetractys).
A topologically related concept is that of triangular numbers, which can be visualized as hexagonally-packed arrangements of circles, hexagons, or dots inside a triangle. Specifically, triangular numbers can be defined as the sum of all natural integers from 1 to n, where n is the number of units per side of the figurate triangle in question. That is, suppose you take three dots and arrange them in a triangle. There are two dots per side of the triangle, and 1+2 = 3. Add another three dots to the base of this triangle and you have another triangle, in this case one with three dots per side, and 1+2+3 = 6 (which also happens to be the product of 1, 2, and 3, as mentioned earlier). And so on. The triangular number of side length n can also be calculated as n*(n+1)/2—thus, 3*(3+1)/2 = 3+2+1 = 6.
 The same figurate hexagonal lattice is also employed by the centered hexagonal numbers, or hex numbers, which are analogous to triangular numbers, but of course with hexagons instead of triangles. (For reasons I have a hard time understanding, the term "hexagonal number" is reserved for a hexagonal outline figure that is not really usefully similar to what is meant by "triangular number" or "square number," at least not in a way that I find particularly interesting.) The nth hex number can be expressed as six times the triangular number of (n – 1) plus one, or as n*(n-1)*3+1, which can be understood as the sum of three rectangles plus the center dot.
The same figurate hexagonal lattice is also employed by the centered hexagonal numbers, or hex numbers, which are analogous to triangular numbers, but of course with hexagons instead of triangles. (For reasons I have a hard time understanding, the term "hexagonal number" is reserved for a hexagonal outline figure that is not really usefully similar to what is meant by "triangular number" or "square number," at least not in a way that I find particularly interesting.) The nth hex number can be expressed as six times the triangular number of (n – 1) plus one, or as n*(n-1)*3+1, which can be understood as the sum of three rectangles plus the center dot.
A further interesting fact about hex numbers is that the sum of the first n hex numbers is equal to the cube of n. For instance, 1+7 = 23 = 8, 1+7+19 = 33 = 27, 1+7+19+37 = 43 = 64, et cetera. To understand this, imagine looking at the corner of a cube, in such a way that the cube looks like a hexagon. Imagine that the cube is actually made up of sub-cubes arranged in the manner of a cubed number. The first cube in the corner can be thought of as the first hex number, which is 1. Below and around this are seven other cubes forming a layer of cubes around the corner cube, which can be thought of as the second hex number, which is in fact 7, and so on. The hex numbers can be thought of as successive "shells" of cubes emanating out from the corner cube. Thus, cubes and hex numbers are merely different figurate ways of describing the same values—the cube of n can be arranged either as a cube or as a pyramid of hexagons with a base length of n, and the difference between any two consecutive cubes is itself a hexagon. Again we see the relationship between the six-sided hexagon and the six-sided cube—and, by extension, between the hexagon and the six "sides" of three-dimensional space itself.
Conclusion
Again, this article has only scratched the surface of the many interesting properties of hexagons and their analogues. Indeed, hexagons pop up in very unusual places in more abstract mathematical systems, and it is my general suspicion that, if you were to map out all the logical relationships of mathematics as humanity has understood and defined them, the hexagon would feature prominently as a recurring theme throughout the entire structure.
As human society advances, we will no doubt find more and more applications for the versatile and efficient hexagon. Whether tessellating our board games, forming our efficiently-enclosed structures, or helping us better understand fundamental mathematical concepts, we will certainly find ourselves living in a more and more hexagonal world as time goes on. Is it any coincidence that science fiction movies and television shows—particularly those set in outer space—often feature hexagonal doors, hexagonal spacecraft, hexagonal architecture, et cetera? I think not. The visionaries and artists of our society have already seen what is coming, and what will be obvious to our descendants: that we live in a hexagonal world, ordered by hexagonal principles. Hexagons may not be a solution to all the world's problems. They may not even be a solution to very many problems at all. But they will be a solution to some problems, and that is more than you can say about a lot of things.
 An Introduction to Hexagonal Geometry
An Introduction to Hexagonal Geometry
Thanks!!
Just a quick shout to say thanks for creating and writing this webpage, it has been a massive help with my physics project!
Re: Q on hexagonal ring pattern algorithm
Question: if one is calculating the proper number of hexagons in each ring of an ever-expanding number of rings, starting with one hexagon in the center, surrounded by six hexagons, those in turn surrounded by 12 hexagons, etc.: is the correct algorithm for each new ring "npr + 6 = nnr", where npr = "number in previous ring" and nnr = "number in new ring"? If so, this gives some interesting prime number results along the way, both in the number of hexagons per ring and the cumulative totals, if my math is correct. Primes that figure in the lunar cycles. Thanks.
Thank you so much for writing this article. It has been so helpful in helping me finish my book which is about destiny. I have been studying sacred geometry and Metatrons Cube for quite some time but this is the only site i believe has the depth of knowledge and ideas to help me complete some pretty difficult chapters.
Thank you so much for making a complex subject (well diverse anyway) into a thoroughly enjoyable one!
Steve
very informative....
Another fact about the relationship between the circle and the hexagon even more revealing than hex-packability. Draw a circle, and keeping your compasses to the same aperture, put the point on the circumference and step round till you're back at the starting point. That's 6 equal arcs. No wonder 6 was such a basic number for star gazing cultures, like the Babylonians, using circular observatory platforms to mark stellar positions, periodicities, and time itself.
Re: Q on hexagonal ring pattern algorithm
I printed off a hexagonal pattern from Google Images and constructed a hexagon spiral (like an Ulam number spiral but with hexagons instead of squares), starting with 1 in the centre. I got a line of interesting primes and composites following the formula given in the "Hexagonal Geometry" text above: n*(n-1)*3+1. They go 1,7,19,37,61,91,127,169 ... I know of 19 and 127 figuring in lunar cycles: the 19 year Metonic cycle and the 127 toothed gear wheel in the Antikythera mechanism. I'd be really interested to hear ones you were thinking of.
Other interesting numerical relationships: 61 is exactly 1/6 of 366, what you get if you round the number of days in a year up instead of down. 91 is 7*13 and n=7 gets you 169, or 13 squared. Some kind of interplay between 7 and 13, the traditionally sacred and unlucky numbers, separated by just 6.
Adjacent to the hex number line in the spiral is a line of 6-multiples generated by the same formula as above without the +1, so n*(n+1)*3. This includes 6 squared, 6 cubed, 6 factorial. And some major Babylonian angle divisions: 60, 90, 270.
Re: Thanks!!
gracias por la informacion
Occupied Ireland? Really?
666 is the devil's number...
Very interesting article though.
This site had the information about hexagons I was looking for and a good number of additional interesting facts. Thanks for putting it together!
666 is not the devils number. It's the number of the beast according to the bible but this is probably wrong :While many Bible have footnotes saying the number translated from the original Greek could be 616, experts say new photographic evidence of an ancient fragment of papyrus from Revelation indeed indicates the number is indeed 616, instead of 666. Read more at http://www.wnd.com/2005/05/30211/#1Iz2mOvC5cZY0gE8.99
hexagon tessellation in xy plot
found very little info on how to do this...took me hours...is there an easier way ...any1? https://www.desmos.com/calculator/dpnxb3hkir
Re: hexagon tessellation in xy plot
this one is "almost" in a single EQ....the plotters list func hides the overlay https://www.desmos.com/calculator/dtwtfliqql
"Likewise, in three dimensions, among uniform polyhedra, only the six-sided cube and the hexagonally-analogous truncated octahedron can form space-filling tessellations by themselves."
Nope, a hrombic dodecahedròn tiles 3D the best, and makes safer nail-free buildings: http://archinstitute.blogspot.com.
THE MYTH OF 666
''666" never existed in biblical times. ( base ten of course) WHY? ...because Hindo-arabic numerals didn't exist then . Greek or Hebrew #s & ROMAN numerals were used.... & this was the time of Roman occupation [succeding the period of Alexander the Great's Hellenistic empire]... If you list all the roman letters used for numbers lower than 1000 [in any order] D/C/L/X/V/I - you will find they add up to six hundred sixty six.. This was merely code for ''the Roman Empire'' / occupation power. nevertheless - there are some interesting properties to that #..... it represents the sum of the 1st (6x6) or 36 integers, for starters.
+ My Email is (36x36) or 6x6x6x6 or 1296 in Roman numerals.
yeah. really.