Close-packing of spheres

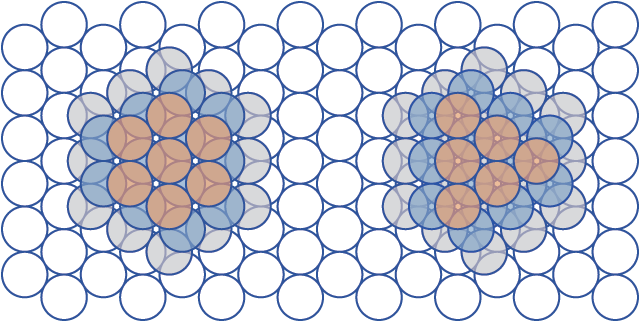
This diagram illustrates both the hexagonal close-packing (left) and face-centered cubic (right) systems for the close-packing of spheres in Euclidean 3-space. Note the hexagonal symmetries of both arrangements. Both can be assembled using the same hexagonally-packed layers—they differ only in how the layers are stacked together.

In each hexagonally-packed layer, there are gaps left between every three spheres. Spheres from the next layer are placed in these gaps. In any given layer, however, one has a choice of which gaps to fill with spheres—only half of the gaps can have spheres in them, since a sphere placed in any particular gap precludes a sphere from being placed in any of the three gaps immediately adjacent to it. Thus, in the hexagonal close-packing system, layers are stacked such that the spheres in each layer align with the spheres two layers below it. In the face-centered cubic system, layers are stacked such that the spheres align with the spheres three layers below it.

If the three possible positions of each layer are labeled A, B, C, then the HCP packing consists of alternating layers of the same type: A, B, A, B, A, B, et cetera, or what have you, while the FCC packing cycles through all three layers: A, B, C, A, B, C, A, B, C, and so on. Along the stacking axis it is possible to switch back and forth between the two packing systems at any time, or indeed to pack the layers in a completely random pattern: A, C, A, B, A, C, B, C, A, B, C, and so on. Madness! Note that the cubic system takes on its eponymous cubic form when looked at from a different angle—in this "layer-on" view, only the hexagonal symmetry is apparent. The hexagonal plane bisects the cubic structure in much the same fashion as a hexagon can be inscribed on the inside of a cube. This is one of several interesting interrelationships between hexagons and cubes, such as the cubic structure of hex numbers.

From Wikipedia:

"In geometry, close-packing of spheres is the construction of an infinite regular arrangement (or lattice) of identical spheres so that they take up the greatest possible fraction of an infinite 3-dimensional space (i.e., they are packed as densely as possible).

"There are two regular lattices that achieve this highest average density. They are called face-centered cubic (FCC) and hexagonal close-packed (HCP), based on their symmetry. Both are based upon sheets of spheres arranged at the vertices of a triangular tiling; they differ in how the sheets are stacked upon one another. In both arrangements each sphere has twelve neighbors. For every sphere there is one gap surrounded by six spheres (octahedral) and two smaller gaps surrounded by four spheres (tetrahedral). The distances to the centers of these gaps from the centers of the surrounding spheres is square root of 3/2 for the tetrahedral, and square root of 2 for the octahedral, when the sphere radius is 1."